Article de blogue

Aucun, un, certains, énormément

5 février 2025

TDD

Et si une technique nous permettait d’aborder un problème complexe, une étape à la fois. Et si chacun de ces problèmes était si petit qu’il en était simple. N’aurions-nous pas de la facilité à résoudre chacun de ceux-ci? N’aurions-nous pas l’énergie de les résoudre un à un avec un rythme soutenu?

Visualisons le travail d’alpinistes sur une montagne. Chaque étape est précédée d’une pause. Ensuite une décision. Et finalement un mouvement délibéré.

Ceci peut donner l’impression d’aller terriblement lentement à première vue. En pratique, c’est une façon de prendre les bonnes décisions, optimiser son parcourt, conserver son énergie et finalement gravir la montagne.

Le TDD se veut être une des approches de ce style.

L’exemple

Le client veut faire un traitement spécial sur les nombres pairs d’une liste d’items.

Voici donc un exemple de ce processus, présenté via un algorithme simplifié qui demande simplement d’extraire des nombres pairs d’une liste d’items.

Aucun

Première étape. Déterminer le comportement quand l’algorithme ne retourne aucun résultat.

[Fact]
public void AucunResultat_QuandListeVide()
{
    chiffresPairs = ObtenirChiffresPairs();

Déjà, nous devons réfléchir au nom de notre fonction ObtenirChiffresPairs.

Ces noms ne seraient-ils pas tout aussi valables?

chiffresPairs = ObtenirChiffresPairs();
    
chiffresPairs = ChiffresPairs();
    
chiffresPairs = FiltrerChiffresImpairs();
    
chiffresPairs = RetirerChiffresImpairs();

Sans avoir écrit une seule ligne de code de production, nous devons déjà déterminer les termes le plus appropriés à notre problème et son domaine.

Exercice qui est encore plus bénéfique en travail en binôme.

Prochaine décision

Quelle devrait être la valeur de retour?

Une liste vide? Un IEnumerable vide? Null*? -1?
Probablement pas NULL. Nous ne voudrions pas perpétuer le billion-dollar mistake.

On décide d’opter pour une liste vide comme ailleurs dans ce système pour s’assurer de préserver l’ordre.

chiffresPairs.Should().BeEmpty();

L’implémentation

public static IList<int> ObtenirChiffresPairs()
{
    return new List<int>();
}

Et le test passe!

Un

Maintenant que nous avons une fonction et un retour, il faudrait commencer à pouvoir traiter des données.

On ajoute ce cas de test:

[Fact]
public void RetourneNombrePair_QuandListerAvecUnSeulElementPair()

Il faut maintenant penser à ce que la fonction prendra en entrée.
Un int[], IEnumerable, IList<int>, params?

On opte pour une IList<int>.

[Fact]
public void RetourneNombrePair_QuandListerAvecUnSeulElementPair()
{
    chiffresPairs = ObtenirChiffresPairs(new List<int>{2});
    
    chiffresPairs.Should().BeEquivalentTo(new List<int>{2});
}

Nous ajustons la signature de la méthode pour devenir ceci.

public static IList<int> ObtenirChiffresPairs(IList<int> chiffres)

Notre IDE nous aide et ajoute ce paramètre au test précédent également.

[Fact]
public void AucunResultat_QuandListeVide()
{
    chiffresPairs = ObtenirChiffresPairs(new List<int>());

Le premier test est vert. Le deuxième rouge. On le fait passer bêtement avec ceci.

public static IList<int> ObtenirChiffresPairs(IList<int> chiffres)
{
    return chiffres;
}

Certains

Maintenant que notre design est fait pour les entrées et sorties et que nous couvrons deux cas spéciaux, il est enfin temps de s’attaquer à la logique d’affaires.

Notre client veut des chiffres pairs et si ce sont des chiffres pairs qu’il veut, ce sont des chiffres pairs qu’on va lui donner!

[Fact]
public void RetourneNombresPair_QuandElementsPairsEtImpairs()
{
    chiffresPairs = ObtenirChiffresPairs(new List<int>{1,2,3,4,5,6,7,8,9});
    
    chiffresPairs.Should().BeEquivalentTo(new List<int>{2,4,6,8});
}

On prend confiance et on fait passer les 3 tests comme ceci:

public static IList<int> ObtenirChiffresPairs(IList<int> chiffres)
{
    return chiffres.Where(x => x % 2 == 0).ToList();
}

Énormément

Make It Work Make It Right Make It Fast — Kent Beck

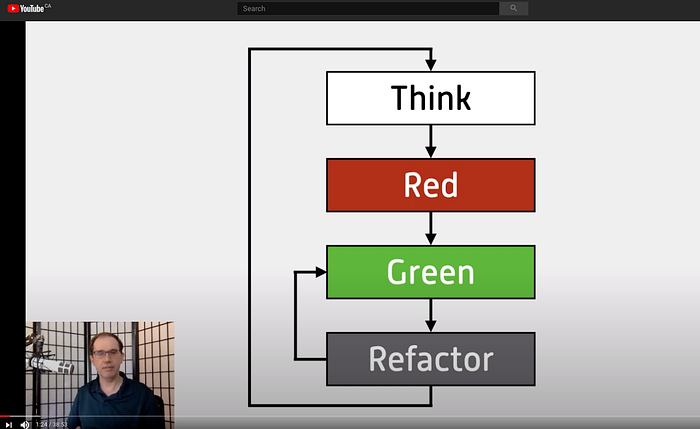
En mode TDD, le cycle de Red -> Green -> Refactor mène typiquement à couvrir les deux premières étapes et ce dans l’ordre suggéré.

Maintenant que ces deux qualités sont atteintes, on peut se questionner sur la possibilité que ce code doive traiter un grand volume de données et se mettre des attentes de performances.

L’efficacité d’un algorithme O(n^x) est rarement un problème si n =1.

Par contre, il peut devenir problématique si soudainement on doit traiter un grand volume.

Un exemple de technique pour prouver la rapidité de notre algorithme.

[Fact]
public async Task Filtre_UnMillionDeChiffres_EnMoinsUnSeconde()
{
    var task = Task.Run(() => ObtenirChiffresPairs(Enumerable.Range(0, 1000000).ToList()));

    var isFastEnough = task.Wait(TimeSpan.FromMilliseconds(1000));
    
isFastEnough
.Should()
.BeTrue("Doit filtrer 1 million en un seconde.");
}

Dans ce cas-ci, nous sommes chanceux et l’algorithme est déjà assez rapide. Sinon, cette vérification peut nous guider à améliorer notre algorithme, ou prévenir des régressions lors de futurs travaux.